Relationship between profit factor and risk per trade

I stumbled upon this discovery by accident.

 

As a general rule of thumb, traders risk 1-2% of their equity per trade to control their drawdown when they lose.

 

It's also another general rule of thumb that if you are using a trading system, you optimise the variables within the system to maximise your profit factor (within reason - if you over-optimise, you end up curve-fitting which has little predictive value).

 

Thus, we trade a system with maximum (or near-maximum) profit factor, and risk 1-2% of our equity per trade.

 

I will explain why this may in fact sub-optimal under certain conditions.

 

I was tinkering with my low-volatility breakout system "Hermes" and found that a reward:risk of 0.5:1 provided a better profit factor than reward:risk of 2:1 (1.49 versus 1.33, respectively). One of the trading mantras you'll find on the internet is "never trade below 2:1!", which is why I tended to disregard any R:R below 1:1.

 

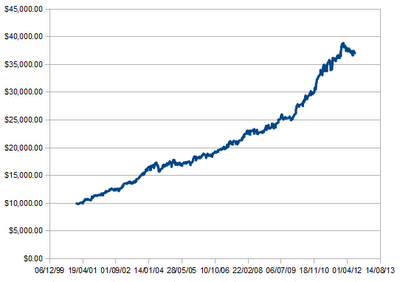
Nevertheless, I decided to plot the equity curves for 2:1 and 0.5:1 R:R, at 1% equity risk per trade. Results are below.

Equity curve for 2-to-1 reward-to-risk, profit factor = 1.33, risking 1% equity per trade.

 

Equity curve for 0.5-to-1 reward-to-risk, profit factor = 1.49, risking 1% equity per trade.

 

As you can see, increasing my profit factor actually harmed the growth of my equity. What's going on!?

 

I spent two days scratching my head, re-checking my maths and wondering what the hell happened. These are two versions of the same system, so the number of trades hasn't changed at all. The only difference between the two system versions was my R:R and nothing else. The system with the higher profit factor should be growing faster, not the other way around.

 

I began to examine my % equity risked per trade, and thought about the Kelly criterion. The Kelly criterion provides a mathematical method of finding your optimal risk per trade. I decided to find the optimal risk level for 2:1 and 0.5:1 R:R, which turned out to be 11% and 28% if I remember correctly.

 

Thus, when my risk was at 1% (when I graphed my equity curve), my risk level is more optimal for 2:1 R:R than 0.5:1 R:R. 1% is closer to 11% than it is to 28%, and thus my equity would grow faster using a R:R of 2:1 than 0.5:1, despite having a lower profit factor.

 

That was a startling discovery, and something I've never read in any trading book so far. It goes to show why a serious trader must do his own homework rather than rely on hearsay from experts or the internet. I'm now wondering if professional traders are aware of this paradox?

 

Now, this dilemma can be solved quite easily if you base your equity risk per trade on some derivative of the Kelly criterion rather than an arbitrary rule like "2%", which is espoused in some trading books. For example, you may risk 10% of Kelly, in which case I would risk 1.1% per trade if I'm using a 2:1 R:R, and 2.8% if I'm using 0.5 R:R. In this case, 0.5 R:R will build equity quicker and all is well.

 

Important lessons:

 

1. Do your own homework

2. Question EVERYTHING, even if it comes from Dr. Alexander Elder (i.e. the 2% rule)

3. Use context-sensitive, self-adjusting rules rather than hard, arbitrary rules